| ◄Назад | Содержание | Вперед► |
Считаем в уме

Плюсы устного счета
Счетным навыкам нас обучают с детства. Это элементарные операции сложения, вычитания, умножения и деления. В случае небольших чисел с ними легко справляются даже младшие школьники, но задача существенно усложняется, когда нужно произвести действие с двузначным или трехзначным числом. Однако с помощью тренировки, несложных упражнений и маленьких хитростей вполне можно подчинить данные операции быстрой умственной обработке.
Возможно, вы спросите, зачем это нужно, ведь существует такая удобная вещь, как калькулятор, а на крайний случай под рукой всегда есть бумага для осуществления вычислений. Быстрый счет в уме дает массу преимуществ:
Экономия времени. Рассчитать стоимость покупок в магазине или кафе и проверить правильность сдачи, опередить одноклассников в решении примера или написании теста — все это возможно, если вы хорошо считаете в уме.
Возможность обратиться к другим аспектам задачи. Зачастую задачи содержат в себе, как минимум, две стороны: чисто арифметическую (действия с числами) и интеллектуально-творческую (выбор подходящего решения для конкретной задачи, нестандартный подход для более быстрого решения и др.). Если школьник недостаточно хорошо и быстро справляется с первой стороной, то от этого страдает вторая: концентрируясь на выполнении арифметической составляющей, ребенок не задумывается над смыслом задачи, может не увидеть подвоха или более простого решения. Если же счетные операции доведены до автоматизма или просто не требуют большого количества времени, то «включается» детальное рассмотрение смысла задачи, появляется возможность применения творческого подхода к ней.
Тренировка интеллекта. Счет в уме позволяет держать интеллект в тонусе, постоянно задействовать мыслительные процессы. Особенно это характерно для действий с большими числами, когда мы подбираем способ для максимального упрощения операции.
Упражнения с таблицами
Упражнения рассчитаны на детей любого возраста, испытывающих затруднения при выполнении операций с простыми числами (одно- и двузначными). Позволяет натренировать навыки устного счета, довести до автоматизма несложные арифметические операции.
Необходимые материалы: для выполнения упражнений понадобится сетка одно- и двузначных чисел. Пример:

Картинка из книги: Посталовский И.З. «Тренировочные таблицы для автоматизации устного счета»
В первом столбце располагаются числа, с которыми нужно выполнять действия. Во втором – ответы на эти действия. С помощью специально вырезанной закладки можно проверить правильность вычисления. Например:
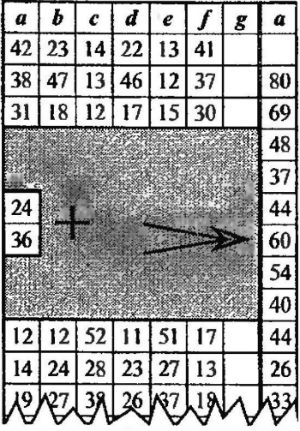
Картинка из книги: Посталовский И.З. «Тренировочные таблицы для автоматизации устного счета»
Варианты упражнений:
Последовательно сложи в уме пары чисел в сетке. Назови ответ вслух и проверь себя с помощью второго столбца и закладки. Задание может выполняться в свободном темпе или на время.
Последовательно выполни вычитание в уме чисел из сетки.
Последовательно сложи в уме пары чисел в сетке. Прибавь к каждой сумме цифру 5 и назови ответ вслух.
Последовательно сложи в уме тройки чисел в сетке.
Последовательно со всеми числами в сетке выполни следующие действия: прибавь нижнее число, из полученной суммы вычти следующую в столбце цифру.
На основе подобных таблиц можно формировать любые задания. Сетки составляются в зависимости от модификации упражнения.
ВАЖНО! Чтобы упражнение дало результат, оно должно выполняться регулярно, до полного усвоения навыка.
Осваиваем умножение
Упражнение предназначено для детей, освоивших таблицу умножения от 1 до 10. Тренирует навык перемножения двузначного числа на однозначное.
Составляется столбик из произвольных двузначных чисел. Задание для ребенка: последовательно умножить эти числа сначала на 1, потом на 2, на 3 и т.д. Ответ произносится вслух. Выполняется до тех пор, пока ответы не запомнятся и не будет выдаваться автоматически.
Главное – внимание
Задание: сложи последовательно числа: 3000 + 2000+ 30 + 2000 + 10 + 20 + 1000 + 10 + 1000 + 30 =
Назови ответ. Проверь себя с помощью калькулятора.
Если ответ получился верным, необходимо закрепить успех и прорешать еще несколько подобных примеров (могут составляться произвольно). Если в ответе была ошибка, нужно вернуться к последовательности чисел и исправить ее.
В чем идея: В результате сложения чисел получается сумма 9100. Но если делать это невнимательно, будет автоматически напрашиваться ответ 10000 (мозг стремится округлить сумму, сделать ответ более красивым). Поэтому очень важно сохранять контроль за своими действиями при производстве арифметических задач в несколько действий.
Возможные примеры:
3000 – 700 — 60 – 500 — 40 – 300 -20 – 100 =
100:2:2*3*2 + 50 – 100 + 200 – 30 =
1*2*3*4*3*2*1 =
26+88+13+19 =
Рекомендации по повышению внимания
Если большинство примеров решается с ошибками (НО! не связанными с умением считать в принципе), то есть смысл повысить концентрацию внимания. Для этого можно:
Минимизировать внешние раздражители. Например, по возможности выйти в другую комнату, выключить музыку, закрыть окно и т.д. Если необходима концентрация на примере во время урока, когда нет возможности выйти и добиться полной тишины, нужно закрыть глаза и представить цифры, с которыми осуществляются действия.
Добавить элемент состязательности. Зная, что верное и быстрое решение принесет победу над противником и/или какое-то поощрение, ученик более охотно сосредоточится на цифрах и предпримет максимум усилий в процессе вычисления.
Устанавливать личные рекорды. Можно визуализировать все ошибки, совершенные школьником в процессе вычисления. Например, нарисовать цветок с крупными лепестками (количество лепестков = количеству решаемых примеров). Черным будет закрашено столько лепестков, сколько примеров было решено с ошибками. Задача – максимально сократить количество черных лепестков, устанавливая личные рекорды с каждой партией примеров.
Небольшие хитрости и советы для быстрого счета
Группировка. Последовательно складывая/вычитая несколько чисел, необходимо посмотреть, какие из них при сложении/вычитании дадут целое число: 13 и 67, 98 и 32, 49 и 11 и т.д. Сначала выполнить действия с этими цифрами, а потом перейти к остальным. Пример:7+65+43+82+64+28=(7+43)+(82+28)+65+64=50+110+124=289
Разложение на десятки и единицы. При умножении двух двузначных чисел (например, 24 и 57) выгодно одно из них (заканчивающееся на меньшую цифру) разложить на десятки и единицы: 24 как 20 и 4. Второе число умножается сначала на десятки (57 на 20), потом на единицы (57 на 4). Затем оба значения складываются. Пример:24×57=57×20+57×4=1140+228=1368
Умножение на 5. При умножении любого числа на 5, выгоднее сначала умножить его на 10, а потом разделить на 2. Пример:45×5=45×10/2=450/2=225
Умножение на 4 и 8. При умножении на 4, выгоднее умножить число два раза на 2; на 8 – три раза на 2. Пример: 63×4=63x2x2=126×2=252
Деление на 4 и 8. Аналогично умножению: при делении на 4 разделить число дважды на 2, на 8 – трижды на 2. Пример:192/8=192/2/2/2=96/2/2=48/2=24
Возведение в квадрат чисел, заканчивающихся на 5. Облегчить это действие позволит следующий алгоритм: число десятков, возводимого в квадрат числа, умножается на такое же плюс единица и приписывается в конце 25. Пример: 75^2=7x(7+1)=7×8=5625
Умножение по формуле. В ряде случаев для облегчения счета можно применить формулу разности квадратов: (a+b)x(a-b)=a^2-b^2. Пример:52×48=(50+2)x(50-2)=50^2-2^2=2500-4=2496
P.S. Данные правила могут существенно упростить устный счет, однако необходимы регулярные тренировки, чтобы в нужный момент можно было правильно воспользоваться правилом. Поэтому рекомендуется прорешать такое количество примеров на каждое из них, которое позволит автоматизировать навык. Для начала можно записывать расчеты на бумаге, постепенно сокращая количество написанного и переводя операции в мыслительный план. В первое время также рекомендуется проверять свои ответы при помощи калькулятора или стандартных вычислений в столбик.
| ◄Назад | Содержание | Вперед► |